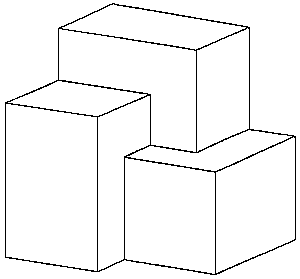
Figure 1. The union of three cuboids.
| Teaching Solid Modelling |
3. Teaching solid modelling using Minimod
Stephen Cameron
Abstract
For several years we have been using a small, CSG-based modelling system called Minimod to teach undergraduate students at Oxford. The course that the students take has two aims: to teach the rudiments of solid modelling and to show, by example, the construction and use of a large computer program.
Introduction
Undergraduate Engineering and Computer Science students at Oxford University take a number of short (one-week) courses at the end of their second year. For three years we have used a small CSG-based geometric modelling system called Minimod as the basis of a project that aims both to teach the rudiments of solid modelling; and to show, by example, the construction and use of a moderately large computer program. The course allows us to take several topics that the students will have seen previously only in an abstract setting, such as program structuring, object-oriented design, linear algebra, and set-theory, and to show how they can all be used within a program that is both technically useful and that produces some nice graphics!
Although boundary modelling systems are more popular in real applications, the use of CSG has some advantages for a course of this nature: simple textual input of interesting shapes is possible; the internal data structures (mainly trees and linked lists) are simpler than for a boundary modeller; and the code is relatively short-just over 5 000 lines of code. The system is implemented in , but with emphasis on readability rather than on using advanced features of the language. There is also a small Tcl/Tk script [4] that acts as the standard graphics driver, although this is easily altered as there are only a small number of low-level graphics functions required, namely:
Course structure
The short-course structure taken by these students allows us to immerse them in a topic for a entire week. This format has the advantage of keeping the students' minds on the topic, but the disadvantage of not giving them much time to mull over what they are learning. The course is thus structured as ten half-day sessions, of about 3-31/2 hours apiece. At the beginning of each session the students are given a lecture of between 30-60 minutes, that introduces the problem that they are to tackle, together with any relevant theory. For the rest of the session the students attempt to solve the problem by adding to the modeller, with help both from a partner and from graduate-student helpers. At the beginning of the first session the students are given a cut-down version of the modeller, with all of the input routines working, but with most of the 'guts' missing. After each session the students can compare their solution with a specimen answer, which also forms the basis for the next session. In this way the students are always dealing with code that does compile, and the changes that they are making at any time are small and localized.
The session topics themselves are chosen both to cover the basics of modelling, and to keep the students interested (with interesting graphics!). The assignments for each session are listed in the Assignments section below.
Using Minimod

Figure 1. The union of three cuboids.
For simplicity, Minimod uses the CSG paradigm to describe objects-that is, shapes are described in terms of parameterized simple shapes, or in terms of set-operations on shapes. For ease of use the program is controlled by typing commands in an interactive fashion, one command to an input line. (Input can also be redirected from input files.) Most command lines take the form of a command word followed by a list of arguments, and an example of user input would be
a = cub(2,3,4
b = cub(3,4,2)
c = cub(4,2,3)
draw a ++ b ++ c
in which the first three lines define three variables, each of which is assigned to a primitive shape (i.e. cuboids with sides of varying lengths), and the last line instructs the system to draw a picture of the union of the three cuboids, as shown in Figure 1. Again, for ease of use the input form is not constrained, and variables can be assigned to complete shape expressions, and so the input
d = cub(2,3,4) ++ cub(3,4,2)
draw d ++ cub(4,2,3)
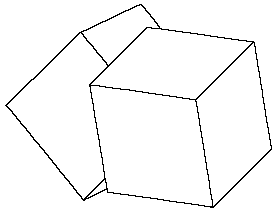
Figure 2. The union of two cubes with various transformations applied.
would have the same effect. The other two set-operations, intersection and difference, are denoted by ** and // respectively. There are also standard transformations available, using the functions to for translation and rotx, roty and rotz for rotation about the coordinate axes; these can be chained or applied to shapes by concatenation on the input line, as in
a = cub(4,4,4)
b = a rotx(45) to(2,2,2)
draw a roty(15) ++ b
the output of which is shown in Figure 2.
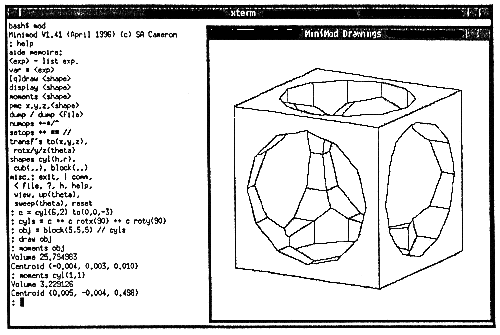
Figure 3. Screen dump of Minimod in action.
Minimod is normally used in an X-Windows environment, with commands being typed into a standard terminal window, and graphics output appearing in another window. An example of this type of use is shown in Figure 3. However the graphics output mechanism used is quite simple, and can easily be converted for other devices-an earlier version of the program was used under DOS on a PC. Graphical output can also be dumped to a printer or file directly from Minimod in encapsulated Postscript format, which is the mechanism used for producing most of the figures in this paper.
Instead of typing commands directly into Minimod, commands can also be stored in files, and read in using a redirection command.
Structure of Minimod
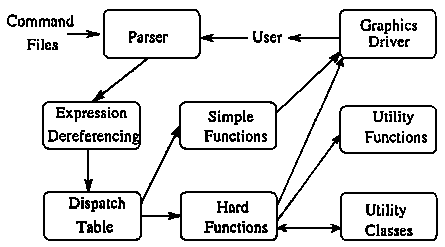
Figure 4. Overall structure of Minimod.
Minimod is implemented in C++, and the overall program structure is shown in Figure 4. Commands entered by the user (or from a command file) are read in using a parser constructed using the standard tools YACC and Lex (or their Gnu equivalents, Bison and Flex). Variable assignment and substitution then occurs in the expression dereferencing stage, after which all expressions exist within Minimod in a fully evaluated form, namely as suitable constants for numbers and strings, as binary trees for shapes, and there is also a linked list type for chains of transformations. The parser then uses a simple dispatch table to call the appropriate function within the heart of Minimod. I have split these functions into two classes in the figure-simple and hard-although this distinction is not really evident within the code.
Simple functions are those that can produce their answer directly from the data-structures that they are given. For example, for each data-structure there is a function that just gives a textual dump of the structure. Another less trivial 'simple function' is the one that draws each primitive shape in a given CSG expression in its correct position, overlaid on the screen. Hard functions, on the other hand, require some detailed geometric computation to occur. These use a second form of CSG tree which makes these computations easier to perform, and use some utility functions. Some of the 'utility functions' are naturally expressed as methods on the appropriate data-structures, and being a C++ program we use C++ class functions to implement these. (Some of the simple functions are also implemented as class functions.)
Part of the purpose of teaching with Minimod is to illustrate the structure of a large computer program, and this need has influenced the detailed structure of the Minimod program. Thus, during the assignments, the students are largely concerned with the implementation of some of the functions (the middle column in Figure 4) and the higher-level utilities (the right column in the figure). We do not show the students the way that the left column works, and we only give them the interface specification for the graphics driver and some of the utility functions and classes.
Assignments
The ten assignments that we currently use are chosen to take our students from the stage in which they have had little or no previous experience of , to being able in principle to sit down and follow the structure of the entire program (other than the parser and expression dereferencer) if they so wish. In fact, several students have chosen to extend Minimod for a major programming project in their third year; they have written ray-tracers, added new primitives, and even a boundary evaluator.
The approach used in the course is best summarized as 'throwing them in at the deep end', and only succeeds due to the high level of support in the practicals, and the fact that most Oxford students are very good! (As a rule of thumb the students are taken from the top 2% of the population, in terms of academic achievement before the age of 18.) A highly motivated group or one that was already familiar with C++ could probably also be pushed at a similar speed, but a more 'normal' group would need to be taken more slowly. The assignments are as follows:
The assignment requires them to complete this process, and to test their code using a textual dump of the new tree (called a 'small nodes tree', as the new tree structure is optimized for the copying operations that will follow.)
The students' reaction to this assignment is that it is simple-they already know how to intersect two planes from linear algebra! They invariably discover that it isn't as simple as it sounds, and the assignment acts as a valuable object lesson in the difficulties of getting geometric computations right.
Using this package they are quickly able to reconstruct their output from the last assignment. Next, they need to be able to classify the type of edge, and to try to determine whether the edge is locally visible. That is, they must determine whether
A full answer to this question would require a proper analysis of the neighbourhood of a slice across the edge, and this is not implemented in Minimod. Instead, they can obtain a simplified CSG tree that describes the neighbourhood using a simple tree rewriting scheme [5], and then examine the simplified tree.
In Cases 2 and 3 a simple face-normal test then suffices to tell whether an edge is locally visible. Case 4 is actually quite rare, as there would have to be more than two planes from the objects cutting the edge.
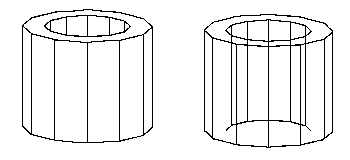
Figure 5. A shape for which local line removal does not work.
The result of the assignment are pictures that look good for many objects. However objects which are self-occluding will not be treated properly-for example, in Figure 5 the cylinder with a hole shown on the left appears as shown on the right.
Conclusions
The standard initial reaction of the students to the course is bewilderment; it really does throw them in at the deep end. However, by the end of the week, most of them find that they get a lot out of the course, even if they do not carry on to do geometric computing; they do get a sense of achievement from being able to find their way around such a large program. Another plus point is the use of (simple) graphics; once they start being able to see the outline of the shapes appearing on a computer screen they become highly motivated to crack the assignments. (Indeed there is a problem getting them to spend enough time on Assignment 8, which does not use graphics, as they prefer to play around further with the result of Assignment 7 instead!)
Given more time, there are several ways in which the course could be extended. One thread could further emphasize the computer science aspects: the parser is more interesting than a standard 'calculator' example, without being particularly big or cumbersome, and much more time could be spent exploring the use of an object-oriented implementation language. Ray-tracing would make another easy addition, but that topic is covered in a separate computer graphics course.
The most obvious way of extending the course to deal with other topics in geometric modelling would be to consider various forms of boundary representation. If we modify the drawing program slightly we can produce all the surface edges, but generally each edge will appear in several pieces, and it is an interesting exercise to stick the pieces together to make whole edges. At this point we could produce wire-frame drawings of the object. Furthermore, for each edge we can easily determine (in most cases) the two faces that bound it, and this will allow polyhedral facets to be generated by use of a scan-line algorithm, and then used for surface display by a polygon engine. The final step, of producing a well linked B-rep structure, is from our experience quite hard to get right, and would probably be best covered in a course in the same way as we do for hidden-line elimination, namely by explaining the theory, but only asking them to fix up a small part of the code. (We have written similar code for our earlier Robmod modeller [1].
References